The Discounted Cash Flow (DCF) model in Excel is like a calculator. It helps figure out how much a company or investment is really worth. It achieves this by assessing the company’s expected future earnings and then knowing its present value.
To achieve this, consider a few factors:
- The company’s potential revenue.
- Its growth rate.
- The present value of money compared to the future.
People who work with finance use the DCF model a lot to decide how much something is worth. This article explains how to use the DCF model in a simple way. It breaks down all the steps so you can do it yourself in Excel. The DCF formula is really important when you’re doing financial planning. Also, it helps a lot when you want to know how much a business is worth.
What is the Discounted Cash Flow?
The Discounted Cash Flow (DCF) method serves as an important tool for financial assessment and investment analysis. It plays a pivotal role in establishing the core value of a company by estimating the present worth of anticipated cash flows. This includes the concept of the time value of money. It also recognizes that cash expected in the future holds a lesser value compared to immediate cash.
Discounted Cash Flow analysis finds broad application across various fields:
Business Valuation: This method enables investors and financial experts to gauge the financial worth of a business when studying investments, acquisitions, or mergers.
Investment Analysis: Investors can employ DCF to assess the appeal of investment prospects, whether they involve stocks, bonds, real estate, or projects. This involves comparing the estimated present value of incoming cash flows to the current expenses.
Capital Budgeting: Companies rely on DCF to make informed decisions regarding capital expenses, including launching new projects or buying equipment. It assists in verifying whether these investments will yield enough cash flows to justify the capital infusion.
Corporate Finance: DCF aids in the allocation of capital, the determination of the cost of capital, and the review of the financial feasibility of strategic projects and initiatives within the corporate realm.
Financial Planning: On a personal level, individuals can employ DCF to evaluate the value of their personal assets, such as retirement plans, investments, or businesses. This serves purposes such as estate planning, succession planning, or wealth management.
The DCF Formula
The DCF formula is a mathematical equation that combines cash flows from different time periods. It involves dividing the cash flow for each period by the result of raising one plus the discount rate (commonly referred to as the WACC) to the power of the same period number.

In this example, we have five periods with the same cash flows. The interest rate or discount rate (r) is not specified, so we can’t calculate the exact discounted cash flow values. However, the table shows how the formula can be applied by computing the discount factor as 1/(1+r)^n and then getting the discounted cash flow by multiplying the cash flow (CF) with the corresponding discount factor.
Please note that without a specific interest rate, the discounted cash flow values are for illustrative purposes only.
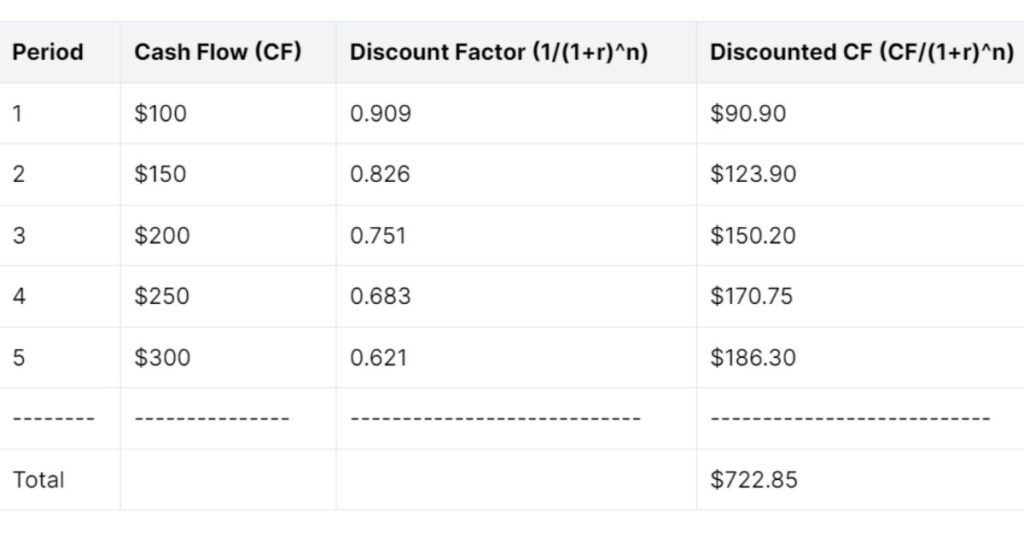
Elements of the Formula
- Cash Flow (CF)
Cash Flow (CF) denotes the total cash disbursements that an investor gains within a specific timeframe as a result of holding a particular financial asset, such as bonds or shares.
When constructing a financial model for a company, people often refer to this cash flow as ‘unlevered free cash flow.’ Meanwhile, when you assess the value of a bond, you include interest and/or principal payments in the cash flow.
- Discount Rate (r)
In the context of business valuation, the discount rate commonly aligns with a company’s Weighted Average Cost of Capital (WACC). WACC is employed by investors as it reflects the expected rate of return they seek when investing in the company.
In the case of a bond, the discount rate equates to the interest rate associated with the security.
- Every cash flow represents a specific time period, which people commonly measure in years, quarters, or months. These time intervals can either be uniform or variable. In cases of variability, people represent them as a percentage of a year.
Insights from the Discounted Cash Flow Formula
When evaluating a prospective investment, it is crucial to consider either the time value of money or the expected rate of return. The Discounted Cash Flow (DCF) formula includes your expected return, determining the amount you would be prepared to invest in order to attain precisely that rate of return.
When the payment is below the DCF (Discounted Cash Flow) value, your rate of return surpasses the discount rate.
If your payment exceeds the discounted cash flow (DCF) value, your rate of return will fall below the discount rate.
Terminal Value
When assessing your business’s value, it is usual to project its annual cash flows for a five-year period ahead, and then include a terminal value. Adopting this approach helps predict a business’s performance reliably beyond this horizon becomes challenging.
There are two common methods for determining the terminal value:
Exit Multiple Method: This method assumes that the business will be sold, and it computes the terminal value based on a specified multiple.
Perpetual Growth Method: In this method, it is assumed that the business will sustain a reasonable, constant growth rate indefinitely.
DCF vs. NPV
The aggregate Discounted Cash Flow (DCF) for an investment is commonly known as the Net Present Value (NPV). When we break down the term NPV, its meaning becomes evident:
Net implies the accumulation of all positive and negative cash flows.
Present value denotes the process of discounting these cash flows to the investment’s initial time.
Discounted Cash Flow in Excel
Microsoft Excel offers two formulas for computing discounted cash flows, referred to as “NPV.”
The first formula is the standard NPV formula, which is as follows:
=NPV(discount rate, series of cash flows)
This formula assumes that all cash inflows are evenly distributed over uniform time periods. It also includes those periods like years, quarters, months, or any other consistent time frame. The discount rate should also align with the timing of these cash flows. This means you should use an annual discount rate of r% for annual cash flows.
On the other hand, there is the Time-Adjusted NPV formula, denoted as XNPV:
=XNPV (discount rate, series of all cash flows, dates of all cash flows)
XNPV proves to be highly useful when you need to discount cash flows received at irregular intervals. This feature is especially valuable in financial modeling scenarios where a company might undergo acquisition or experience non-standard cash flow timing.
How to Compute in Excel
For instance, consider a situation where the initial investment occurs on June 15th, the next cash inflow on December 31st, and the following cash flows each year apart. In this case, XNPV is the tool you need to efficiently handle these calculations in Excel.
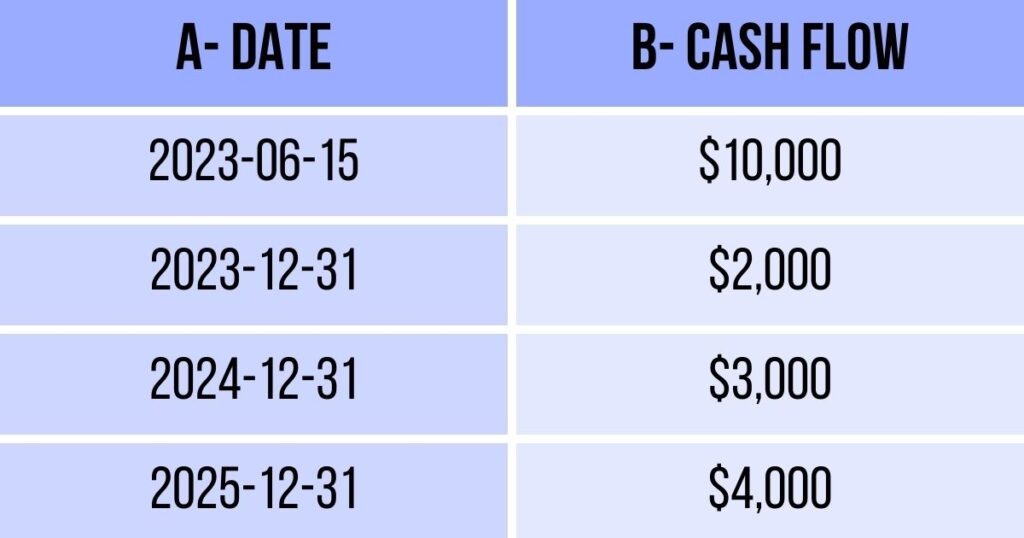
Let’s walk through the computation of the Time-Adjusted NPV (XNPV) for a set of cash flows received at irregular intervals using an example. In this example, we have the following cash flows:
Initial investment on June 15, 2023: $10,000
Cash flow on December 31, 2023: $2,000
Cash flow on December 31, 2024: $3,000
Cash flow on December 31, 2025: $4,000
Assuming a discount rate of 5%, we want to compute the XNPV.
Here’s how you can compute it in Excel:
In an Excel spreadsheet, create a table with two columns: one for the dates of cash flows and another for the corresponding cash flow amounts.
Next, in a cell where you want to calculate the XNPV, enter the following formula:
=XNPV(0.05, B2:B5, A2:A5)
The 0.05 represents the 5% discount rate.B2:B5 refers to the cash flow amounts in cells B2 through B5.A2:A5 refers to the corresponding dates in cells A2 through A5. Press Enter, and Excel will calculate the XNPV, which should be approximately $18,484.54.
This XNPV value represents the present value of the irregular cash flows at a 5% discount rate. It takes into account the varying dates of cash flows. This results in a more accurate calculation of the net present value when cash flows are unevenly distributed.
Conclusion
The Discounted Cash Flow (DCF) method serves as a crucial tool in financial analysis, allowing us to verify the present value of expected future cash flows. By considering factors such as expected earnings, growth rates, and the time value of money, the DCF model aids professionals in various financial domains. It plays a central role in knowing the worth of investments and projects.
Moreover, Microsoft Excel offers both standard NPV and Time-Adjusted NPV (XNPV) formulas to accommodate different cash flow patterns, allowing for precise valuation even when cash flows occur irregularly. Mastering these tools empowers individuals and organizations to make informed financial decisions, ensuring that they accurately assess the true value of their investments and ventures.
In general, using Excel based formulas and software tools that integrate with Excel to help consolidate and analyze data can save you lots of time and energy. This will free up more time for strategic decision making.
According to research and analysis from Solving Finance, the top 2 Excel based FP&A software are:





